Topological sorting

This example demonstrates how to get a topological sorting on a directed acyclic graph (DAG). A topological sorting of a directed graph is a linear ordering based on the precedence implied by the directed edges. It exists iff the graph doesn’t have any cycle. In igraph, we can use igraph.GraphBase.topological_sorting() to get a topological ordering of the vertices.

import igraph as ig
import matplotlib.pyplot as plt

First off, we generate a directed acyclic graph (DAG):

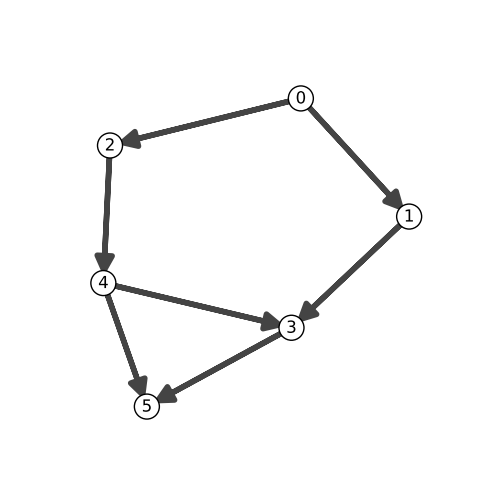
g = ig.Graph(
    edges=[(0, 1), (0, 2), (1, 3), (2, 4), (4, 3), (3, 5), (4, 5)],
    directed=True,
)

We can verify immediately that this is actually a DAG:

assert g.is_dag

A topological sorting can be computed quite easily by calling igraph.GraphBase.topological_sorting(), which returns a list of vertex IDs. If the given graph is not DAG, the error will occur.

results = g.topological_sorting(mode='out')
print('Topological sort of g (out):', *results)

Topological sort of g (out): 0 1 2 4 3 5

In fact, there are two modes of igraph.GraphBase.topological_sorting(), 'out' 'in'. 'out' is the default and starts from a node with indegree equal to 0. Vice versa, 'in' starts from a node with outdegree equal to 0. To call the other mode, we can simply use:

results = g.topological_sorting(mode='in')
print('Topological sort of g (in):', *results)

Topological sort of g (in): 5 3 1 4 2 0

We can use igraph.Vertex.indegree() to find the indegree of the node.

for i in range(g.vcount()):
    print('degree of {}: {}'.format(i, g.vs[i].indegree()))

# %
# Finally, we can plot the graph to make the situation a little clearer.
# Just to change things up a bit, we use the matplotlib visualization mode
# inspired by `xkcd <https://xkcd.com/>_:
with plt.xkcd():
    fig, ax = plt.subplots(figsize=(5, 5))
    ig.plot(
        g,
        target=ax,
        layout='kk',
        vertex_size=25,
        edge_width=4,
        vertex_label=range(g.vcount()),
        vertex_color="white",
    )

degree of 0: 0
degree of 1: 1
degree of 2: 1
degree of 3: 2
degree of 4: 1
degree of 5: 2