Tutorial (Español)

Esta página es un tutorial detallado de las capacidades de igraph para Python. Para obtener una impresión rápida de lo que igraph puede hacer, consulte el Quick Start. Si aún no ha instalado igraph, siga las instrucciones de Installing igraph.

Note

Para el lector impaciente, vea la página Gallery of Examples para ejemplos cortos y autocontenidos.

Comenzar con igraph

La manera más común de usar igraph es como una importanción con nombre dentro de un ambiente de Python (por ejemplo, un simple shell de Python, a IPython shell, un Jupyter notebook o una instancia JupyterLab, Google Colab, o un IDE):

$ python
Python 3.9.6 (default, Jun 29 2021, 05:25:02)
[Clang 12.0.5 (clang-1205.0.22.9)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> import igraph as ig

Para llamar a funciones, es necesario anteponerles el prefijo ig (o el nombre que hayas elegido):

>>> import igraph as ig
>>> print(ig.__version__)
0.9.8

Note

Es posible utilizar importación con asterisco para igraph:

>>> from igraph import *

pero en general se desaconseja <https://stackoverflow.com/questions/2386714/why-is-import-bad>`_.

Hay una segunda forma de iniciar igraph, que consiste en llamar al script igraph desde tu terminal:

$ igraph
No configuration file, using defaults
igraph 0.9.6 running inside Python 3.9.6 (default, Jun 29 2021, 05:25:02)
Type "copyright", "credits" or "license" for more information.
>>>

Note

Para los usuarios de Windows encontrarán el script dentro del subdirectorio file:scripts de Python y puede que tengan que añadirlo manualmente a su ruta.

Este script inicia un intérprete de comandos apropiado (IPython o IDLE si se encuentra, de lo contrario un intérprete de comandos Python puro) y utiliza importación con asterisco (véase más arriba). Esto es a veces conveniente para usar las funciones de igraph.

Note

Puede especificar qué shell debe utilizar este script a través Configuration de igraph.

Este tutorial asumirá que has importado igraph usando el de nombres ig.

Creando un grafo

La forma más sencilla de crear un grafo es con el constructor Graph. Para hacer un grafo vacío:

>>> g = ig.Graph()

Para hacer un grafo con 10 nodos (numerados 0 to 9) y dos aristas que conecten los nodos 0-1 y 0-5:

>>> g = ig.Graph(n=10, edges=[[0, 1], [0, 5]])

Podemos imprimir el grafo para obtener un resumen de sus nodos y aristas:

>>> print(g)
IGRAPH U--- 10 2 --
+ edges:
0--1 0--5

Tenemos entonces: grafo no dirigido (U**ndirected) con **10 vértices y 2 aristas, que se enlistan en la última parte. Si el grafo tiene un atributo “nombre”, también se imprime.

Note

summary es similar a print pero no enlista las aristas, lo cual es conveniente para grafos grandes con millones de aristas:

>>> summary(g)
IGRAPH U--- 10 2 --

Añadir y borrar vértices y aristas

Empecemos de nuevo con un grafo vacío. Para añadir vértices a un grafo existente, utiliza Graph.add_vertices():

>>> g = ig.Graph()
>>> g.add_vertices(3)

En igraph, los vértices se numeran siempre a partir de cero El número de un vértice es el ID del vértice. Un vértice puede tener o no un nombre.

Del mismo modo, para añadir aristas se utiliza Graph.add_edges():

>>> g.add_edges([(0, 1), (1, 2)])

Las aristas se añaden especificando el vértice origen y el vértice destino de cada arista. Esta llamada añade dos aristas, una que conecta los vértices 0 y 1, y otra que conecta los vértices 1 y 2. Las aristas también se numeran a partir de cero (el ID del arista) y tienen un nombre opcional.

Warning

Crear un grafo vacío y añadir vértices y aristas como se muestra aquí puede ser mucho más lento que crear un grafo con sus vértices y aristas como se ha demostrado anteriormente. Si la velocidad es una preocupación, deberías evitar especialmente añadir vértices y aristas de uno en uno. Si necesitas hacerlo de todos modos, puedes usar Graph.add_vertex() y Graph.add_edge().

Si intentas añadir aristas a vértices con IDs no válidos (por ejemplo, intentas añadir una arista al vértice 5 cuando el grafo sólo tiene tres vértices), obtienes un error igraph.InternalError:

>>> g.add_edges([(5, 4)])
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "/usr/lib/python3.10/site-packages/igraph/__init__.py", line 376, in add_edges
    res = GraphBase.add_edges(self, es)
igraph._igraph.InternalError: Error at src/graph/type_indexededgelist.c:270: cannot add edges. -- Invalid vertex id

El mensaje intenta explicar qué ha fallado (cannot add edges. -- Invalid vertex id) junto con la línea correspondiente del código fuente en la que se ha producido el error.

Note

El rastreo completo, incluida la información sobre el código fuente, es útil cuando se informa de errores en nuestro Página de problemas de GitHub. Por favor, inclúyalo completo si crea un nuevo asunto.

Añadamos más vértices y aristas a nuestro grafo:

>>> g.add_edges([(2, 0)])
>>> g.add_vertices(3)
>>> g.add_edges([(2, 3), (3, 4), (4, 5), (5, 3)])
>>> print(g)
IGRAPH U---- 6 7 --
+ edges:
0--1 1--2 0--2 2--3 3--4 4--5 3--5

Ahora tenemos un grafo no dirigido con 6 vértices y 7 aristas. Los IDs de los vértices y aristas son siempre continuos, por lo que si eliminas un vértice todos los vértices subsiguientes serán renumerados. Cuando se renumera un vértice, las aristas no se renumeran, pero sí sus vértices de origen y destino. Utilice Graph.delete_vertices() y Graph.delete_edges() para realizar estas operaciones. Por ejemplo, para eliminar la arista que conecta los vértices 2-3, obten sus IDs y luego eliminalos:

>>> g.get_eid(2, 3)
3
>>> g.delete_edges(3)

Generar grafos

igraph incluye generadores de grafos tanto deterministas como estocásticos. Los generadores deterministas producen el mismo grafo cada vez que se llama a la función, por ejemplo:

>>> g = ig.Graph.Tree(127, 2)
>>> summary(g)
IGRAPH U--- 127 126 --

Utiliza Graph.Tree() para generar un grafo regular en forma de árbol con 127 vértices, cada vértice con dos hijos (y un padre, por supuesto). No importa cuántas veces llames a Graph.Tree(), el grafo generado será siempre el mismo si utilizas los mismos parámetros:

>>> g2 = ig.Graph.Tree(127, 2)
>>> g2.get_edgelist() == g.get_edgelist()
True

El fragmento de código anterior también muestra el método get_edgelist(), que devuelve una lista de vértices de origen y destino para todas las aristas, ordenados por el ID de la arista. Si imprimes los 10 primeros elementos, obtienes:

>>> g2.get_edgelist()[:10]
[(0, 1), (0, 2), (1, 3), (1, 4), (2, 5), (2, 6), (3, 7), (3, 8), (4, 9), (4, 10)]

Los generadores estocásticos producen un grafo diferente cada vez; por ejemplo, Graph.GRG():

>>> g = ig.Graph.GRG(100, 0.2)
>>> summary(g)
IGRAPH U---- 100 516 --
+ attr: x (v), y (v)

Note

+ attr` muestra atributos para vértices (v) y aristas (e), en este caso dos atributos de vértice y ningún atributo de arista.

Esto genera un grafo geométrico aleatorio: Se eligen n puntos de forma aleatoria y uniforme dentro del cuadrado unitario y los pares de puntos más cercanos entre sí respecto a una distancia predefinida d se conectan mediante una arista. Si se generan GRGs con los mismos parámetros, serán diferentes:

>>> g2 = ig.Graph.GRG(100, 0.2)
>>> g.get_edgelist() == g2.get_edgelist()
False

Una forma un poco más relajada de comprobar si los grafos son equivalentes es mediante isomorphic():

>>> g.isomorphic(g2)
False

Comprobar por el isomorfismo puede llevar un tiempo en el caso de grafos grandes (en este caso, la respuesta puede darse rápidamente comprobando las distribuciones de grados de los dos grafos).

Establecer y recuperar atributos

Como se ha mencionado anteriormente, en igraph cada vértice y cada arista tienen un ID numérico de 0 en adelante. Por lo tanto, la eliminación de vértices o aristas puede causar la reasignación de los ID de vértices y/o aristas. Además de los IDs, los vértices y aristas pueden tener atributos como un nombre, coordenadas para graficar, metadatos y pesos. El propio grafo puede tener estos atributos también (por ejemplo, un nombre, que se mostrará en print o Graph.summary()). En cierto sentido, cada Graph, vértice y arista pueden utilizarse como un diccionario de Python para almacenar y recuperar estos atributos.

Para demostrar el uso de los atributos, creemos una red social sencilla:

>>> g = ig.Graph([(0,1), (0,2), (2,3), (3,4), (4,2), (2,5), (5,0), (6,3), (5,6)])

Cada vértice representa una persona, por lo que queremos almacenar nombres, edades y géneros:

>>> g.vs["name"] = ["Alice", "Bob", "Claire", "Dennis", "Esther", "Frank", "George"]
>>> g.vs["age"] = [25, 31, 18, 47, 22, 23, 50]
>>> g.vs["gender"] = ["f", "m", "f", "m", "f", "m", "m"]
>>> g.es["is_formal"] = [False, False, True, True, True, False, True, False, False]

Graph.vs y Graph.es son la forma estándar de obtener una secuencia de todos los vértices y aristas respectivamente. El valor debe ser una lista con la misma longitud que los vértices (para Graph.vs) o aristas (para Graph.es). Esto asigna un atributo a todos los vértices/aristas a la vez.

Para asignar o modificar un atributo para un solo vértice/borde, puedes hacer lo siguiente:

>>> g.es[0]["is_formal"] = True

De hecho, un solo vértice se representa mediante la clase Vertex, y una sola arista mediante Edge. Ambos, junto con Graph, pueden ser tecleados como un diccionario para establecer atributos, por ejemplo, para añadir una fecha al grafo:

>>> g["date"] = "2009-01-10"
>>> print(g["date"])
2009-01-10

Para recuperar un diccionario de atributos, puedes utilizar Graph.attributes(), Vertex.attributes() y Edge.attributes().

Además, cada Vertex tiene una propiedad especial, Vertex.index, que se utiliza para averiguar el ID de un vértice. Cada Edge tiene Edge.index más dos propiedades adicionales, Edge.source y Edge.target, que se utilizan para encontrar los IDs de los vértices conectados por esta arista. Para obtener ambas propiedades a la vez, puedes utilizar Edge.tuple.

Para asignar atributos a un subconjunto de vértices o aristas, puedes utilizar el corte:

>>> g.es[:1]["is_formal"] = True

La salida de g.es[:1] es una instancia de EdgeSeq, mientras que VertexSeq es la clase equivalente que representa subconjuntos de vértices.

Para eliminar atributos, puedes utilizar del, por ejemplo:

>>> g.vs[3]["foo"] = "bar"
>>> g.vs["foo"]
[None, None, None, 'bar', None, None, None]
>>> del g.vs["foo"]
>>> g.vs["foo"]
Traceback (most recent call last):
  File "<stdin>", line 25, in <module>
KeyError: 'Attribute does not exist'

Warning

Los atributos pueden ser objetos arbitrarios de Python, pero si está guardando grafos en un archivo, sólo se conservarán los atributos de cadena (“string”) y numéricos. Consulte el módulo pickle de la biblioteca estándar de Python si busca una forma de guardar otros tipos de atributos. Puede hacer un pickle de sus atributos individualmente, almacenarlos como cadenas y guardarlos, o puedes hacer un pickle de todo el Graph si sabes que quieres cargar el grafo en Python.

Propiedades estructurales de los grafos

Además de las funciones simples de manipulación de grafos y atributos descritas anteriormente, igraph proporciona un amplio conjunto de métodos para calcular varias propiedades estructurales de los grafos. Está más allá del alcance de este tutorial documentar todos ellos, por lo que esta sección sólo presentará algunos de ellos con fines ilustrativos. Trabajaremos con la pequeña red social que construimos en la sección anterior.

Probablemente, la propiedad más sencilla en la que se puede pensar es el “grado del vértice” (vertex degree). El grado de un vértice es igual al número de aristas incidentes a él. En el caso de los grafos dirigidos, también podemos definir el grado de entrada (in-degree, el número de aristas que apuntan hacia el vértice) y el grado de salida (out-degree, el número de aristas que se originan en el vértice):

>>> g.degree()
[3, 1, 4, 3, 2, 3, 2]

Si el grafo fuera dirigido, habríamos podido calcular los grados de entrada y salida por separado utilizando g.degree(mode="in") y g.degree(mode="out"). También puedes usar un único ID de un vértice o una lista de ID de los vértices a degree() si quieres calcular los grados sólo para un subconjunto de vértices:

>>> g.degree(6)
2
>>> g.degree([2,3,4])
[4, 3, 2]

Este procedimiento se aplica a la mayoría de las propiedades estructurales que igraph puede calcular. Para las propiedades de los vértices, los métodos aceptan un ID o una lista de IDs de los vértices (y si se omiten, el valor predeterminado es el conjunto de todos los vértices). Para las propiedades de las aristas, los métodos también aceptan un único ID de o una lista de IDs de aristas. En lugar de una lista de IDs, también puedes proporcionar una instancia VertexSeq o una instancia EdgeSeq apropiadamente. Más adelante, en el próximo capítulo “consulta de vértices y aristas”, aprenderás a restringirlos exactamente a los vértices o aristas que quieras.

Note

Para algunos casos, no tiene sentido realizar el calculo sólo para unos pocos vértices o aristas en lugar de todo el grafo, ya que de todas formas se tardaría el mismo tiempo. En este caso, los métodos no aceptan IDs de vértices o aristas, pero se puede restringir la lista resultante más tarde usando operadores estándar de indexación y de corte. Un ejemplo de ello es la centralidad de los vectores propios (Graph.evcent())

Además de los grados, igraph incluye rutinas integradas para calcular muchas otras propiedades de centralidad, como la intermediación de vértices y aristas o el PageRank de Google (Graph.pagerank()), por nombrar algunas. Aquí sólo ilustramos la interrelación de aristas:

>>> g.edge_betweenness()
[6.0, 6.0, 4.0, 2.0, 4.0, 3.0, 4.0, 3.0. 4.0]

Ahora también podemos averiguar qué conexiones tienen la mayor centralidad de intermediación con un poco de magia de Python:

>>> ebs = g.edge_betweenness()
>>> max_eb = max(ebs)
>>> [g.es[idx].tuple for idx, eb in enumerate(ebs) if eb == max_eb]
[(0, 1), (0, 2)]

La mayoría de las propiedades estructurales también pueden ser obtenidas para un subconjunto de vértices o aristas o para un solo vértice o arista llamando al método apropiado de la clase VertexSeq o EdgeSeq de interés:

>>> g.vs.degree()
[3, 1, 4, 3, 2, 3, 2]
>>> g.es.edge_betweenness()
[6.0, 6.0, 4.0, 2.0, 4.0, 3.0, 4.0, 3.0. 4.0]
>>> g.vs[2].degree()
4

Busqueda de vértices y aristas basada en atributos

Selección de vértices y aristas

Tomando como ejemplo la red social anterirormente creada, te gustaría averiguar quién tiene el mayor grado o centralidad de intermediación. Puedes hacerlo con las herramientas presentadas hasta ahora y conocimientos básicos de Python, pero como es una tarea común seleccionar vértices y aristas basándose en atributos o propiedades estructurales, igraph te ofrece una forma más fácil de hacerlo:

>>> g.vs.select(_degree=g.maxdegree())["name"]
['Claire']

La sintaxis puede parecer un poco rara a primera vista, así que vamos a tratar de interpretarla paso a paso. meth:~VertexSeq.select es un método de VertexSeq y su único propósito es filtrar un VertexSeq basándose en las propiedades de los vértices individuales. La forma en que filtra los vértices depende de sus argumentos posicionales y de palabras clave. Los argumentos posicionales (los que no tienen un nombre explícito como _degree siempre se procesan antes que los argumentos de palabra clave de la siguiente manera:

• Si el primer argumento posicional es None, se devuelve una secuencia vacía (que no contiene vértices):

  >>> seq = g.vs.select(None)
  >>> len(seq)
  0
  

• Si el primer argumento posicional es un objeto invocable (es decir, una función, un método vinculado o cualquier cosa que se comporte como una función), el objeto será llamado para cada vértice que esté actualmente en la secuencia. Si la función devuelve True, el vértice será incluido, en caso contrario será excluido:

  >>> graph = ig.Graph.Full(10)
  >>> only_odd_vertices = graph.vs.select(lambda vertex: vertex.index % 2 == 1)
  >>> len(only_odd_vertices)
  5
  

• Si el primer argumento posicional es un iterable (es decir, una lista, un generador o cualquier cosa sobre la que se pueda iterar), debe devolver enteros y estos enteros se considerarán como índices del conjunto de vértices actual (que no es necesariamente todo el grafo). Sólo se incluirán en el conjunto de vértices filtrados los vértices que coincidan con los índices dados. Los numero flotantes, las cadenas y los ID de vértices no válidos seran omitidos:

  >>> seq = graph.vs.select([2, 3, 7])
  >>> len(seq)
  3
  >>> [v.index for v in seq]
  [2, 3, 7]
  >>> seq = seq.select([0, 2])         # filtering an existing vertex set
  >>> [v.index for v in seq]
  [2, 7]
  >>> seq = graph.vs.select([2, 3, 7, "foo", 3.5])
  >>> len(seq)
  3
  

• Si el primer argumento posicional es un número entero, se espera que todos los demás argumentos sean también números enteros y se interpretan como índices del conjunto de vértices actual. Esto solo es “azucar sintáctica”, se podría conseguir un efecto equivalente pasando una lista como primer argumento posicional, de esta forma se pueden omitir los corchetes:

  >>> seq = graph.vs.select(2, 3, 7)
  >>> len(seq)
  3
  

Los argumentos clave (“keyword argument”) pueden utilizarse para filtrar los vértices en función de sus atributos o sus propiedades estructurales. El nombre de cada argumento clave consiste como máximo de dos partes: el nombre del atributo o propiedad estructural y el operador de filtrado. El operador puede omitirse; en ese caso, automáticamente se asume el operador de igualdad. Las posibilidades son las siguientes (donde name indica el nombre del atributo o propiedad):

Keyword argument	Significado
name_eq	El valor del atributo/propiedad debe ser igual a
name_ne	El valor del atributo/propiedad debe no ser igual a
name_lt	El valor del atributo/propiedad debe ser menos que
name_le	El valor del atributo/propiedad debe ser inferior o igual a
name_gt	El valor del atributo/propiedad debe ser mayor que
name_ge	El valor del atributo/propiedad debe ser mayor o igual a
name_in	El valor del atributo/propiedad debe estar incluido en, el cual tiene que ser una secuencia en este caso
name_notin	El valor del atributo/propiedad debe no estar incluido en , el cual tiene que ser una secuencia en este caso

Por ejemplo, el siguiente comando te da las personas menores de 30 años en nuestra red social imaginaria:

>>> g.vs.select(age_lt=30)

Note

Debido a las restricciones sintácticas de Python, no se puede utilizar la sintaxis más sencilla de g.vs.select(edad < 30), ya que en Python sólo se permite que aparezca el operador de igualdad en una lista de argumentos.

Para ahorrarte algo de tecleo, puedes incluso omitir el método select() si desea:

>>> g.vs(age_lt=30)

También hay algunas propiedades estructurales especiales para seleccionar los aristas:

• Utilizando _source or _from en función de los vértices de donde se originan las aristas. Por ejemplo, para seleccionar todas las aristas procedentes de Claire (que tiene el índice de vértice 2):

  >>> g.es.select(_source=2)
  

• Usar los filtros _target o _to en base a los vértices de destino. Esto es diferente de _source and _from si el grafo es dirigido.

• _within toma un objeto VertexSeq o un set de vértices y selecciona todos los aristas que se originan y terminan en un determinado set de vértices. Por ejemplo, la siguiente expresión selecciona todos los aristas entre Claire (índice 2), Dennis (índice 3) y Esther (índice 4):

  >>> g.es.select(_within=[2,3,4])
  

• _between toma una tupla que consiste en dos objetos VertexSeq o una listas que contienen los indices de los vértices o un objeto Vertex y selecciona todas las aristas que se originan en uno de los conjuntos y terminan en el otro. Por ejemplo, para seleccionar todas las aristas que conectan a los hombres con las mujeres:

  >>> men = g.vs.select(gender="m")
  >>> women = g.vs.select(gender="f")
  >>> g.es.select(_between=(men, women))
  

Encontrar un solo vértice o arista con algunas propiedades

En muchos casos buscamos un solo vértice o arista de un grafo con algunas propiedades, sin importar cuál de las coincidencias se devuelve, ya sea si éxiste mútliples coincidencias, o bien sabemos de antemano que sólo habrá una coincidencia. Un ejemplo típico es buscar vértices por su nombre en la propiedad name. Los objetos VertexSeq y EdgeSeq proveen el método find() para esos casos. Esté método funciona de manera similar a select(), pero devuelve solo la primer coincidencia si hay multiples resultados, y señala una excepción si no se encuentra ninguna coincidencia. Por ejemplo, para buscar el vértice correspondiente a Claire, se puede hacer lo siguiente:

>>> claire = g.vs.find(name="Claire")
>>> type(claire)
igraph.Vertex
>>> claire.index
2

La búsqueda de un nombre desconocido dará lugar a una excepción:

>>> g.vs.find(name="Joe")
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: no such vertex

Búsqueda de vértices por nombres

Buscar vértices por su nombre es una operación muy común, y normalmente es mucho más fácil recordar los nombres de los vértices de un grafo que sus IDs. Para ello, igraph trata el atributo name de los vértices de forma especial; se indexan de forma que los vértices se pueden buscar por sus nombre. Para hacer las cosas incluso más fácil, igraph acepta nombres de vértices (casi) en cualquier lugar dónde se espere especificar un ID de un vérice, e incluso, acepta colecciones (tuplas,listas,etc.) de nombres de vértices dónde sea que se esperé una lista de IDs de vértices. Por ejemplo, puedes buscar el grado (número de conexiones) de Dennis de la siguiente manera:

>>> g.degree("Dennis")
3

o alternativamente:

>>> g.vs.find("Dennis").degree()
3

El mapeo entre los nombres de los vértices y los IDs es mantenido de forma transparente por igraph en segundo plano; cada vez que el grafo cambia, igraph también actualiza el mapeo interno. Sin embargo, la singularidad de los nombres de los vértices no se impone; puedes crear fácilmente un grafo en el que dos vértices tengan el mismo nombre, pero igraph sólo devolverá uno de ellos cuando los busques por nombres, el otro sólo estará disponible por su índice.

Tratar un grafo como una matriz de adyacencia

La matriz de adyacencia es otra forma de formar un grafo. En la matriz de adyacencia, las filas y columnas están etiquetadas por los vértices del grafo: los elementos de la matriz indican si los vértices i y j tienen una arista común (i, j). La matriz de adyacencia del grafo de nuestra red social imaginaria es:

>>> g.get_adjacency()
Matrix([
  [0, 1, 1, 0, 0, 1, 0],
  [1, 0, 0, 0, 0, 0, 0],
  [1, 0, 0, 1, 1, 1, 0],
  [0, 0, 1, 0, 1, 0, 1],
  [0, 0, 1, 1, 0, 0, 0],
  [1, 0, 1, 0, 0, 0, 1],
  [0, 0, 0, 1, 0, 1, 0]
])

Por ejemplo, Claire ([1, 0, 0, 1, 1, 1, 0]) está directamente conectada con Alice (que tiene el índice 0), Dennis (índice 3), Esther (índice 4) y Frank (índice 5), pero no con Bob (índice 1) ni con George (índice 6).

Diseños (“layouts”) y graficar

Un grafo es un objeto matemático abstracto sin una representación específica en el espacio 2D o 3D. Esto significa que cuando queremos visualizar un grafo, tenemos que encontrar primero un trazado de los vértices a las coordenadas en el espacio bidimensional o tridimensional, preferiblemente de una manera que sea agradable a la vista. Una rama separada de la teoría de grafos, denominada dibujo de grafos, trata de resolver este problema mediante varios algoritmos de disposición de grafos. igraph implementa varios algoritmos de diseño y también es capaz de dibujarlos en la pantalla o en un archivo PDF, PNG o SVG utilizando la libreria Cairo.

Important

Para seguir los ejemplos de esta sección, se requieren de la librería Cairo en Python o matplotlib.

Algoritmos de diseños (“layouts”)

Los métodos de diseño en igraph se encuentran en el objeto Graph, y siempre comienzan con layout_. La siguiente tabla los resume:

Method name	Short name	Algorithm description
layout_circle	circle, circular	Disposición determinista que coloca los vértices en un círculo
layout_drl	drl	El algoritmo [Distributed Recursive Layout] para grafos grandes
layout_fruchterman_reingold	fr	El algoritmo dirigido Fruchterman-Reingold
layout_fruchterman_reingold_3d	fr3d, fr_3d	El algoritmo dirigido Fruchterman-Reingold en tres dimensiones
layout_kamada_kawai	kk	El algoritmo dirigido Kamada-Kawai
layout_kamada_kawai_3d	kk3d, kk_3d	El algoritmo dirigido Kamada-Kawai en tres dimensiones
layout_lgl	large, lgl, large_graph	El algoritmo [Large Graph Layout] para grafos grandes
layout_random	random	Coloca los vértices de forma totalmente aleatoria
layout_random_3d	random_3d	Coloca los vértices de forma totalmente aleatoria en 3D
layout_reingold_tilford	rt, tree	Diseño de árbol de Reingold-Tilford, útil para grafos (casi) arbóreos
layout_reingold_tilford_circular	rt_circular tree	Diseño de árbol de Reingold-Tilford con una post-transformación de coordenadas polares, útil para grafos (casi) arbóreos
layout_sphere	sphere, spherical, circular_3d	Disposición determinista que coloca los vértices de manera uniforme en la superficie de una esfera

Los algoritmos de diseño pueden ser llamados directamente o utilizando layout():

>>> layout = g.layout_kamada_kawai()
>>> layout = g.layout("kamada_kawai")

El primer argumento del método layout() debe ser el nombre corto del algoritmo de diseño (mirar la tabla anterior). Todos los demás argumentos posicionales y de palabra clave se pasan intactos al método de diseño elegido. Por ejemplo, las dos llamadas siguientes son completamente equivalentes:

>>> layout = g.layout_reingold_tilford(root=[2])
>>> layout = g.layout("rt", [2])

Los métodos de diseño devuelven un objeto Layout que se comporta principalmente como una lista de listas. Cada entrada de la lista en un objeto Layout corresponde a un vértice en el grafo original y contiene las coordenadas del vértice en el espacio 2D o 3D. Los objetos Layout también contienen algunos métodos útiles para traducir, escalar o rotar las coordenadas en un lote. Sin embargo, la principal utilidad de los objetos Layout es que puedes pasarlos a la función plot() junto con el grafo para obtener un dibujo en 2D.

Dibujar un grafo utilizando un diseño (“layout”)

Por ejemplo, podemos trazar nuestra red social imaginaria con el algoritmo de distribución Kamada-Kawai de la siguiente manera:

>>> layout = g.layout("kk")
>>> ig.plot(g, layout=layout)

Esto debería abrir un visor de imágenes externo que muestre una representación visual de la red, algo parecido a lo que aparece en la siguiente figura (aunque la colocación exacta de los nodos puede ser diferente en su máquina, ya que la disposición no es determinista):

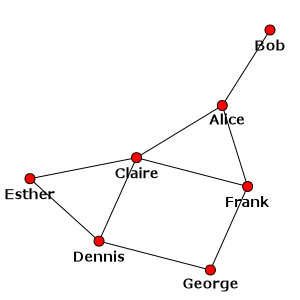
Nuestra red social con el algoritmo de distribución Kamada-Kawai

Si prefiere utilizar matplotlib como motor de trazado, cree un eje y utilice el argumento target:

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> ig.plot(g, layout=layout, target=ax)

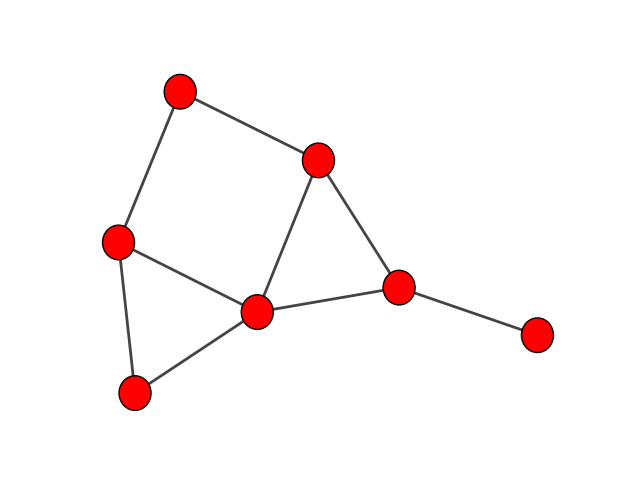
Hmm, esto no es demasiado bonito hasta ahora. Una adición trivial sería usar los nombres como etiquetas de los vértices y colorear los vértices según el género. Las etiquetas de los vértices se toman del atributo label por defecto y los colores de los vértices se determinan por el atributo color:

>>> g.vs["label"] = g.vs["name"]
>>> color_dict = {"m": "blue", "f": "pink"}
>>> g.vs["color"] = [color_dict[gender] for gender in g.vs["gender"]]
>>> ig.plot(g, layout=layout, bbox=(300, 300), margin=20)  # Cairo backend
>>> ig.plot(g, layout=layout, target=ax)  # matplotlib backend

Tenga en cuenta que aquí simplemente estamos reutilizando el objeto de diseño anterior, pero también hemos especificado que necesitamos un gráfico más pequeño (300 x 300 píxeles) y un margen mayor alrededor del grafo para que quepan las etiquetas (20 píxeles). El resultado es:

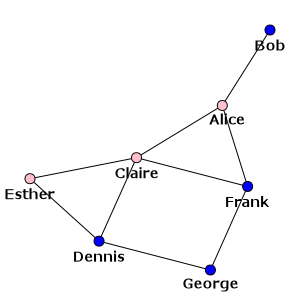
Nuestra red social - con nombres como etiquetas y géneros como colores

y para matplotlib:

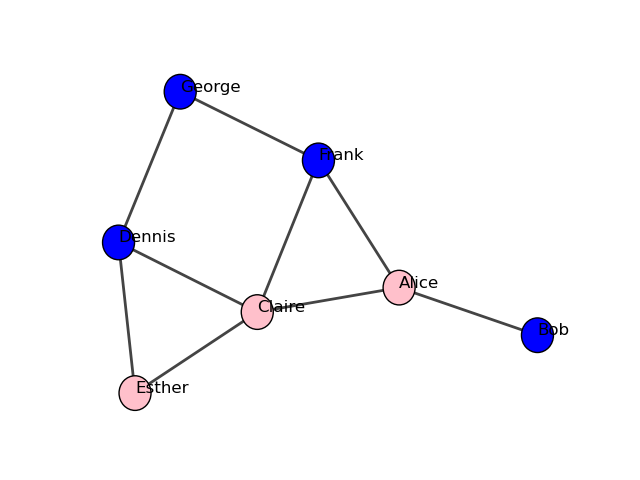
En lugar de especificar las propiedades visuales como atributos de vértices y aristas, también puedes darlas como argumentos a plot():

>>> color_dict = {"m": "blue", "f": "pink"}
>>> ig.plot(g, layout=layout, vertex_color=[color_dict[gender] for gender in g.vs["gender"]])

Este último enfoque es preferible si quiere mantener las propiedades de la representación visual de su gráfico separadas del propio gráfico. Puedes simplemente crear un diccionario de Python que contenga los argumentos que contenga las palabras clave que pasarias a la función plot() y luego usar el doble asterisco (**) para pasar tus atributos de estilo específicos a plot():

>>> visual_style = {}
>>> visual_style["vertex_size"] = 20
>>> visual_style["vertex_color"] = [color_dict[gender] for gender in g.vs["gender"]]
>>> visual_style["vertex_label"] = g.vs["name"]
>>> visual_style["edge_width"] = [1 + 2 * int(is_formal) for is_formal in g.es["is_formal"]]
>>> visual_style["layout"] = layout
>>> visual_style["bbox"] = (300, 300)
>>> visual_style["margin"] = 20
>>> ig.plot(g, **visual_style)

El gráfico final muestra los vínculos formales con líneas gruesas y los informales con líneas finas:

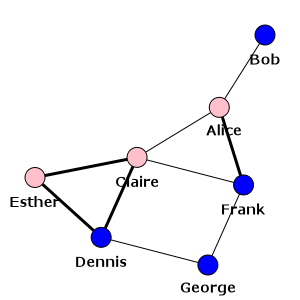
Nuestra red social - también muestra qué vínculos son formales

Para resumirlo todo: hay propiedades especiales de vértices y aristas que corresponden a la representación visual del grafo. Estos atributos anulan la configuración por defecto de igraph (es decir, el color, el peso, el nombre, la forma, el diseño, etc.). Las dos tablas siguientes resumen los atributos visuales más utilizados para los vértices y las aristas, respectivamente:

Atributos de los vértices que controlan los gráficos

Attribute name	Keyword argument	Purpose
color	vertex_color	Color del vertice
font	vertex_font	Familia tipográfica del vértice
label	vertex_label	Etiqueta del vértice.
label_angle	vertex_label_angle	Define la posición de las etiquetas de los vértices, en relación con el centro de los mismos. Se interpreta como un ángulo en radianes, cero significa ‘a la derecha’.
label_color	vertex_label_color	Color de la etiqueta del vértice
label_dist	vertex_label_dist	Distancia de la etiqueta del vértice, en relación con el tamaño del vértice
label_size	vertex_label_size	Tamaño de letra de la etiqueta de vértice
order	vertex_order	Orden de dibujo de los vértices. Vértices con un parámetro de orden menor se dibujarán primero.
shape	vertex_shape	La forma del vértice,. Algunas formas: rectangle, circle, hidden, triangle-up, triangle-down. Ver drawing.known_shapes.
size	vertex_size	El tamaño del vértice en pixels

Atributos de las aristas que controlan los gráficos

Attribute name	Keyword argument	Purpose
color	edge_color	Color de la arista.
curved	edge_curved	La curvatura de la arista. Valores positivos corresponden a aristas curvadas en sentido contrario a las manecillas del reloj, valores negativos lo contrario. Una curvatura cero representa aristas rectas. True significa una curvatura de 0.5, False es una curvatura de cero.
font	edge_font	Familia tipográfica del arista.
arrow_size	edge_arrow_size	Tamaño (longitud) de la punta de flecha del arista si el grafo es dirigido, relativo a 15 pixels.
arrow_width	edge_arrow_width	El ancho de las flechas. Relativo a 10 pixels.
loop_size	edge_loop_size	Tamaño de los bucles. Puede ser negativo para escalar con el tamaño del vertice correspondiente. Este atributo no es utilizado para otras aristas. Este atributo sólo existe en el backend matplotlib.
width	edge_width	Anchura del borde en píxeles.
label	edge_label	Si se especifica, añade una etiqueta al borde.
background	edge_background	Si se especifica, añade una caja rectangular alrededor de la etiqueta de borde (solo en matplotlib).
align_label	edge_align_label	Si es verdadero, gira la etiqueta de la arista de forma que se alinee con la dirección de la arista. Las etiquetas que estarían al revés se voltean (sólo matplotlib).

Argumentos genéricos de plot()

Estos ajustes se pueden especificar como argumentos de palabra clave a la función plot para controlar la apariencia general del gráfico.

Keyword argument	Purpose
autocurve	Determinación automática de la curvatura de las aristas en grafos con múltiples aristas. El estandar es True para grafos con menos de 10000 aristas y False para el caso contrario.
bbox	La caja delimitadora del gráfico. Debe ser una tupla que contenga la anchura y la altura deseadas del gráfico. Por default el gráfico tiene 600 pixels de ancho y 600 pixels de largo.
layout	El diseño que se va a utilizar. Puede ser una instancia de layout una lista de tuplas que contengan coordenadas X-Y, o el nombre un algoritmo de diseño. El valor por defecto es auto, que selecciona un algoritmo de diseño automáticamente basado en el tamaño y la conectividad del grafo.
margin	La cantidad de espacio vacío debajo, encima, a la izquierda y a la derecha del gráfico.

Especificación de colores en los gráficos

igraph entiende las siguientes especificaciones de color siempre que espera un color (por ejemplo, colores de aristas, vértices o etiquetas en los respectivos atributos):

*Nombres de colores X11*

Consulta la lista de nombres de colores X11 en Wikipedia para ver la lista completa. Los nombres de los colores no distinguen entre mayúsculas y minúsculas en igraph, por lo que "DarkBLue" puede escribirse también como "darkblue".

*Especificación del color en la sintaxis CSS*

Se trata de una cadena según uno de los siguientes formatos (donde R, G y B denotan los componentes rojo, verde y azul, respectivamente):

• #RRGGBB, los componentes van de 0 a 255 en formato hexadecimal. Ejemplo: "#0088ff"

• #RGB, los componentes van de 0 a 15 en formato hexadecimal. Ejemplo: "#08f"

• rgb(R, G, B), los componentes van de 0 a 255 o de 0% a 100%. Ejemplo: "rgb(0, 127, 255)" o "rgb(0%, 50%, 100%)".

Guardar gráficos

igraph puede usarse para crear gráficos de calidad de publicación solicitando la función plot() que guarde el gráfico en un archivo en lugar de mostrarlo en pantalla. Para ello, basta con pasar el nombre del archivo destino como argumento adicional después del grafo mismo. El formato preferido se deduce de la extensión. igraph puede guardar en cualquier cosa que soporte Cairo, incluyendo archivos SVG, PDF y PNG. Los archivos SVG o PDF pueden ser convertidos posteriormente al formato PostScript (.ps) o PostScript encapsulado (.eps) si lo prefieres, mientras que los archivos PNG pueden ser convertidos a TIF (.tif):

>>> ig.plot(g, "social_network.pdf", **visual_style)

Si estas usando matplotlib, puedes guardar el gŕafico como de costumbre:

>>> fig, ax = plt.subplots()
>>> ig.plot(g, **visual_style)
>>> fig.savefig("social_network.pdf")

Muchos formatos de archivos son admitidos por matplotlib.

igraph y el mundo exterior

Ningún módulo de grafos estaría completo sin algún tipo de funcionalidad de importación/exportación que permita al paquete comunicarse con programas y kits de herramientas externos. igraph no es una excepción: proporciona funciones para leer los formatos de grafos más comunes y para guardar objetos Graph en archivos que obedezcan estas especificaciones de formato. La siguiente tabla resume los formatos que igraph puede leer o escribir:

Format	Short name	Reader method	Writer method
Adjacency list	lgl	Graph.Read_Lgl()	Graph.write_lgl()
(a.k.a. LGL)
Adjacency matrix	adjacency	Graph.Read_Adjacency()	Graph.write_adjacency()
DIMACS	dimacs	Graph.Read_DIMACS()	Graph.write_dimacs()
DL	dl	Graph.Read_DL()	not supported yet
Edge list	edgelist, edges, edge	Graph.Read_Edgelist()	Graph.write_edgelist()
GraphViz	graphviz, dot	not supported yet	Graph.write_dot()
GML	gml	Graph.Read_GML()	Graph.write_gml()
GraphML	graphml	Graph.Read_GraphML()	Graph.write_graphml()
Gzipped GraphML	graphmlz	Graph.Read_GraphMLz()	Graph.write_graphmlz()
LEDA	leda	not supported yet	Graph.write_leda()
Labeled edgelist	ncol	Graph.Read_Ncol()	Graph.write_ncol()
(a.k.a. NCOL)
Pajek format	pajek, net	Graph.Read_Pajek()	Graph.write_pajek()
Pickled graph	pickle	Graph.Read_Pickle()	Graph.write_pickle()

Como ejercicio, descarga la representación gráfica del conocido Estudio del club de karate de Zacarías en formato graphml. Dado que se trata de un archivo GraphML, debe utilizar el método de lectura GraphML de la tabla anterior (asegúrese de utilizar la ruta adecuada al archivo descargado):

>>> karate = ig.Graph.Read_GraphML("zachary.graphml")
>>> ig.summary(karate)
IGRAPH UNW- 34 78 -- Zachary's karate club network

Si quieres convertir el mismo grafo a, digamos, el formato de Pajek, puedes hacerlo con el método de la tabla anterior:

>>> karate.write_pajek("zachary.net")

Note

La mayoría de los formatos tienen sus propias limitaciones; por ejemplo, no todos pueden almacenar atributos. Tu mejor opción es probablemente GraphML o GML si quieres guardar los grafos de igraph en un formato que pueda ser leído desde un paquete externo y quieres preservar los atributos numéricos y de cadena. La lista de aristas y NCOL también están bien si no tienes atributos (aunque NCOL soporta nombres de vértices y pesos de aristas). Si no quieres utilizar grafos fuera de igraph, pero quieres almacenarlos para una sesión posterior, el formato de grafos pickled te garantza que obtendras exactamente el mismo grafo. El formato de grafos pickled usa el modulo pickle de Python para guardar y leer grafos.

También existen dos métodos de ayuda: read() es un punto de entrada genérico para los métodos de lectura que intenta deducir el formato adecuado a partir de la extensión del archivo. Graph.write() es lo contrario de read(): permite guardar un grafo en el que el formato preferido se deduce de nuevo de la extensión. La detección del formato de read() y Graph.write() se puede anular mediante el argumento format de la palabra clave (“keyword”), la cual acepta los nombres cortos de los otros formatos de la tabla anterior:

>>> karate = ig.load("zachary.graphml")
>>> karate.write("zachary.net")
>>> karate.write("zachary.my_extension", format="gml")

Dónde ir a continuación

Este tutorial sólo ha arañado la superficie de lo que igraph puede hacer. Los planes a largo plazo son ampliar este tutorial para convertirlo en una documentación adecuada de estilo manual para igraph en los próximos capítulos. Un buen punto de partida es la documentación de la clase Graph. Si te quedas atascado, intenta preguntar primero en nuestro Discourse group - quizás haya alguien que pueda ayudarte inmediatamente.