Note
Go to the end to download the full example code.
Shortest Paths
This example demonstrates how to find the shortest distance between two vertices of a weighted or an unweighted graph.
import igraph as ig
import matplotlib.pyplot as plt
To find the shortest path or distance between two nodes, we can use igraph.GraphBase.get_shortest_paths(). If we’re only interested in counting the unweighted distance, then we can do the following:
g = ig.Graph(
6,
[(0, 1), (0, 2), (1, 3), (2, 3), (2, 4), (3, 5), (4, 5)]
)
results = g.get_shortest_paths(1, to=4, output="vpath")
# results = [[1, 0, 2, 4]]
We can print the result of the computation:
if len(results[0]) > 0:
# The distance is the number of vertices in the shortest path minus one.
print("Shortest distance is: ", len(results[0])-1)
else:
print("End node could not be reached!")
Shortest distance is: 3
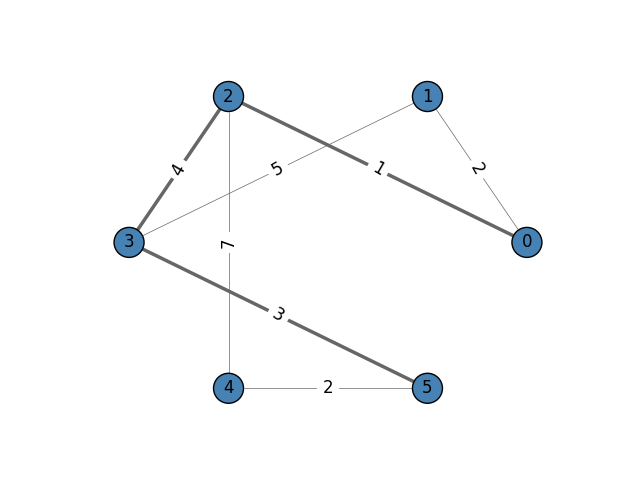
If the edges have weights, things are a little different. First, let’s add weights to our graph edges:
g.es["weight"] = [2, 1, 5, 4, 7, 3, 2]
To get the shortest paths on a weighted graph, we pass the weights as an
argument. For a change, we choose the output format as "epath" to
receive the path as an edge list, which can be used to calculate the length
of the path.
results = g.get_shortest_paths(0, to=5, weights=g.es["weight"], output="epath")
# results = [[1, 3, 5]]
if len(results[0]) > 0:
# Add up the weights across all edges on the shortest path
distance = 0
for e in results[0]:
distance += g.es[e]["weight"]
print("Shortest weighted distance is: ", distance)
else:
print("End node could not be reached!")
Shortest weighted distance is: 8
Note
igraph.GraphBase.get_shortest_paths()returns a list of lists becuase the to argument can also accept a list of vertex IDs. In that case, the shortest path to all each vertex is found and stored in the results array.If you’re interested in finding all shortest paths, take a look at
igraph.GraphBase.get_all_shortest_paths().
In case you are wondering how the visualization figure was done, here’s the code:
g.es['width'] = 0.5
g.es[results[0]]['width'] = 2.5
fig, ax = plt.subplots()
ig.plot(
g,
target=ax,
layout='circle',
vertex_color='steelblue',
vertex_label=range(g.vcount()),
edge_width=g.es['width'],
edge_label=g.es["weight"],
edge_color='#666',
edge_align_label=True,
edge_background='white'
)
plt.show()
Total running time of the script: (0 minutes 0.213 seconds)